Crittografia Visuale
Crittografia Visuale: panoramica sulle principali tecniche e implementazioni. Si tratta di codificare immagini in modo tale che la decodifica può essere effettuata dal sistema visivo umano.

Cryptography is typically bypassed, not penetrated. - Adi Shamir
In molti sostengono ormai da tempo che il cervello umano un giorno sarà in grado di sostituire un computer. Anche se potrebbe sembrare irreale, in un certo senso, ciò è in parte possibile (da più di vent'anni!). Nel 1994, infatti, Moni Naor e Adi Shamir introdussero la crittografia visuale (VC). Si tratta di una tecnica crittografica particolare che permette di codificare informazioni visuali (immagini) in modo tale che la decodifica può essere effettuata dal sistema visivo umano, senza l'ausilio di alcun dispositivo digitale.

In questo articolo vedremo una breve panoramica sulle principali tecniche di crittografia visuale esistenti in letteratura per diverse tipologie di immagini (binarie, a scala di grigi, a colori) e ne proporremo delle implementazioni. Queste ultime sono tratte da un lavoro, svolto da me e il mio caro amico e collega G.T., che prende il nome di VCrypture - per un po' di tempo terremo una demo online disponibile a questo indirizzo. Il codice completo è reperibile al seguente repository Github.
VC vs Crittografia
L'operazione di cifratura classica prevede una stringa (plaintext) e una chiave (key) da prendere in input e, come output, restituisce un crittotesto (cyphertext). Ognuno di questi tre elementi è designato ad un compito ben preciso, dunque se dovessimo scambiare i ruoli della key con il cyphertext e fornire in input all'algoritmo di decifratura la coppia invertita - ammesso che chiave e crittotesto abbiano la stessa lunghezza e possano essere intercambiati dal punto di vista sintattico -, il risultato che otterremmo sarebbe certamente qualcosa di incomprensibile. Riassumendo, la chiave deve adempiere al ruolo di chiave e al tempo stesso il crittotesto deve mantenere il compito di crittotesto. Tuttavia, negli schemi di crittografia visuale che analizzeremo a breve, vedremo che il concetto di chiave e di crittogramma sono del tutto intercambiabili - si noti che in quanto immagini sostituiamo il suffisso -testo con il suffisso -gramma. In particolare, data un'immagine in input (l'equivalente del plaintext) per la cifratura, otterremo due o più immagini delle stesse dimensioni (non necessariamente dell'immagine di input), dette share. Non c'è modo di distinguere lo share chiave dagli share crittogramma, in quanto questi sono del tutto intercambiabili. Per tale motivo è più corretto riferirsi con i termini share_A, share_B, ecc., in generale, in quanto la semantica di chiave o crittogramma è attribuibile a essi in modo soggettivo.
La differenza sostanziale, però, che contraddistingue la crittografia visuale da quella classica sta nel fatto che il processo di decifratura non necessita di alcuna computazione. A breve capiremo meglio come il sistema visivo umano riesca a sostituire un calcolatore per effettuare la decodifica di un'immagine.
Tecniche di Crittografia Visuale
Nei prossimi paragrafi presenteremo una descrizione degli schemi di crittografia visuale che abbiamo incluso nel progetto VCrypture e ne descriveremo le relative implementazioni in Python. Per ognuno degli schemi è disponibile un modulo dal nome omonimo degli autori, all'interno della componente VCrypture-API.
Binary VC

Naor e Shamir si chiesero se fosse possibile dividere un'immagine in n parti in modo che una persona avente tutte le n parti potesse essere in grado di ricostruire l'immagine di partenza, ma qualunque insieme di n-1 parti non rivelasse alcuna informazione. Gli autori pubblicarono l'articolo Visual Cryptogrphy nel quale presentarono proprio questa tecnica. Lo schema Naor-Shamir risulta sicuro fin quando una chiave non verrà riusata più di una volta. In altre parole, la tecnica di crittografia visuale proposta dagli autori è l'equivalente "visuale" di OTP (One-Time-Pad), classico algoritmo crittografico dimostrabile sicuro nel caso in cui la chiave di cifratura venga utilizzata una sola volta. Ricordiamo che OTP utilizza l'operatore XOR. In questo paragrafo presentiamo un'implementazione dell'algoritmo di Naor-Shamir con un numero di share pari a 2. L'algorimo è lossy, in quanto l'immagine di input viene convertita in moalità binaria per poter eseguire le successive operazioni correttamente.
L'algoritmo di cifratura associa ad ogni pixel due matrici 2x2, le quali forniscono i due share del pixel. Ogni matrice deve inoltre avere 2 pixel neri e 2 bianchi. In modo analogo, possiamo dire che ognuno dei pixel dell'immagine di partenza verrà suddiviso in quattro sottopixel, una volta per il primo share e un'altra per il secondo share. In tal modo verranno costruiti, pixel per pixel, i due share che, visti separatamente non hanno alcun significato - ogni share apparirà come se fosse composto da solo rumore sale e pepe. Le dimensioni degli share risulteranno, dunque, il doppio dell'immagine di partenza. La regola da seguire per assegnare i valori dei pixel nelle immagini share è molto semplice: se il pixel dell'immagine originale è nero, le matrici 2x2 negli share devono essere complementari. Quando queste sono sovrapposte, come risultato apparirà proprio il colore nero.
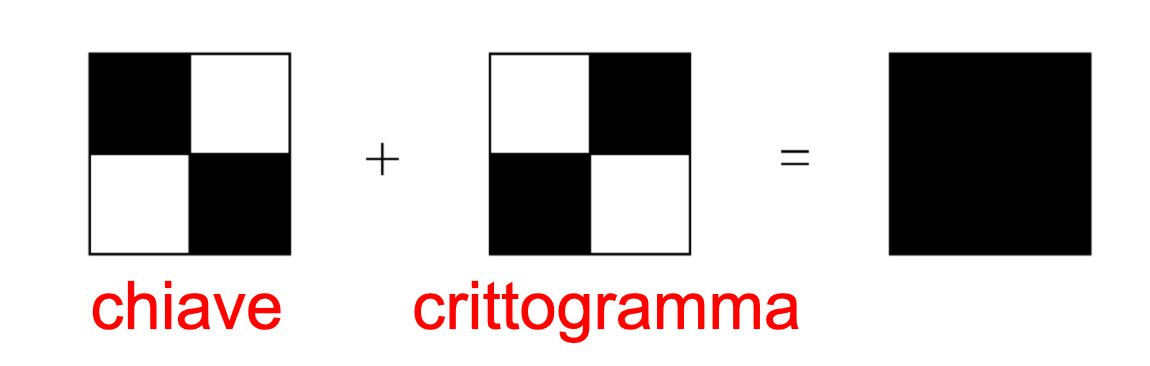
Viceversa, se il pixel dell'immagine originale è bianco, le quadruple di pixel negli share devono corrispondere. Stavolta però, quando le due matrici 2x2 sono sovrapposte, come risultato si otterrà un grigio. È bene evidenziare che l'occhio umano interpolerà il risultato e lo interpreterà come bianco.
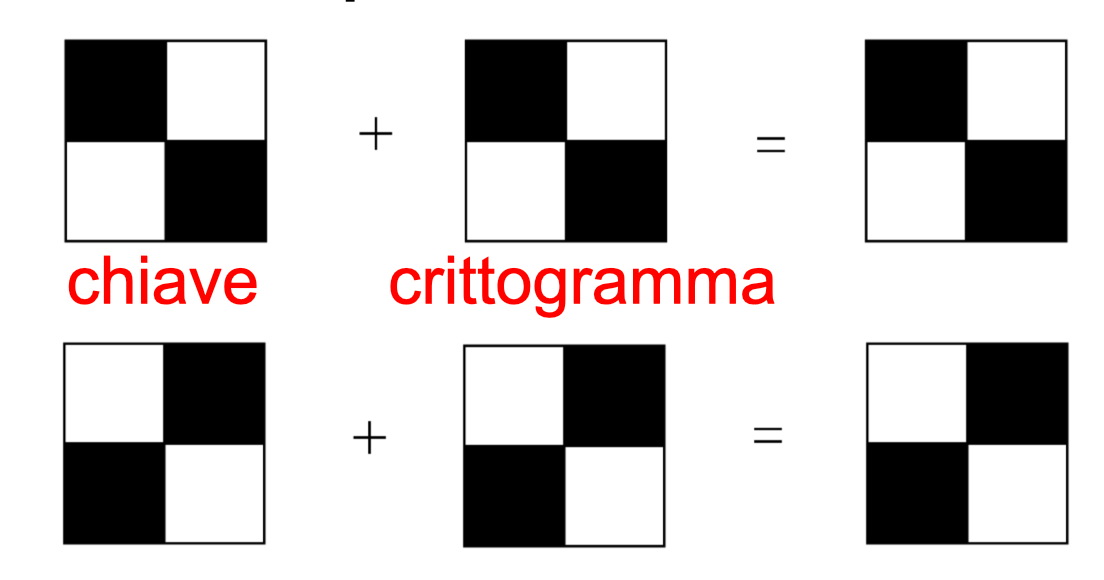
Di seguito è riportato il frammento di codice relativo alle operazioni appena descritte:
patterns = ((1, 1, 0, 0), (1, 0, 1, 0), (1, 0, 0, 1), (0, 1, 1, 0),
(0, 1, 0, 1), (0, 0, 1, 1))
with Image.open(source) as secret:
# Convert the input image to binary
secret = secret.convert('1')
# Prepare the two shares
(width, height) = secret.size
share_size = tuple(s * 2 for s in secret.size)
share_A = Image.new('1', share_size)
draw_A = ImageDraw.Draw(share_A)
share_B = Image.new('1', share_size)
draw_B = ImageDraw.Draw(share_B)
# Cycle through pixels
for x in range(width):
for y in range(height):
pixel = secret.getpixel((x, y))
pat = random.choice(patterns)
# Share A will always get the pattern
draw_A.point((x * 2, y * 2), pat[0])
draw_A.point((x * 2 + 1, y * 2), pat[1])
draw_A.point((x * 2, y * 2 + 1), pat[2])
draw_A.point((x * 2 + 1, y * 2 + 1), pat[3])
if pixel == 0: # B gets the anti-pattern
draw_B.point((x * 2, y * 2), 1 - pat[0])
draw_B.point((x * 2 + 1, y * 2), 1 - pat[1])
draw_B.point((x * 2, y * 2 + 1), 1 - pat[2])
draw_B.point((x * 2 + 1, y * 2 + 1), 1 - pat[3])
else:
draw_B.point((x * 2, y * 2), pat[0])
draw_B.point((x * 2 + 1, y * 2), pat[1])
draw_B.point((x * 2, y * 2 + 1), pat[2])
draw_B.point((x * 2 + 1, y * 2 + 1), pat[3])L'algoritmo di decifratura è molto semplice in quanto simula la sovrapposizione manuale, e quindi l'interpolazione dell'occhio umano, dei due share:
# Overlap shares to get the secret
secret = Image.new('1', share_A.size)
secret_draw = ImageDraw.Draw(secret)
for x in range(secret.size[0]):
for y in range(secret.size[1]):
p1 = share_A.getpixel((x, y)) & 1
p2 = share_B.getpixel((x, y)) & 1
secret_draw.point((x, y), p1 & p2)In aggiunta allo schema 2x2 è possibile estendere la tecnica originale a quattro livelli di grigio, utilizzando matrici 3x3, e così via. È anche possibile utilizzare uno schema a soglia in cui un'immagine viene codificata in N share tali che qualunque K (K<N) share sovrapposti permettano di ottenere l'immagine, mentre un numero minore di K no. Riparleremo di schema a soglia nel paragrafo dedicato alle immagini a colori.
Grayscale VC

L'idea originale di Naor e Shamir può essere estesa anche in altri modi, come viene ad esempio illustrato nell'articolo Visual Cryptography for Gray-scale Images Using Bit-level di Taghaddos e Latif. Dalle immagini binarie facciamo qui un salto a quelle in scala di grigi. Taghaddos-Latif utilizza lo stesso size multiplier di Naor-Shamir e, anche in questo caso, il risultato dell'algoritmo di cifratura è composto da due immagini share. Ne segue che anche questo schema è lossy.
L'algoritmo di cifratura utilizza gli stessi pattern dello schema precedente. La complicazione in più è dovuta al fatto che adesso non si lavora più con valori binari, ma a scala di grigi con 8 bit (bitplane), dunque bisogna aggiungere un ulteriore ciclo per scorrere gli 8 bit di ogni pixel:
patterns = ((1, 1, 0, 0), (1, 0, 1, 0), (1, 0, 0, 1), (0, 1, 1, 0),
(0, 1, 0, 1), (0, 0, 1, 1))
with Image.open(source) as secret:
# Enforce grayscale mode
if secret.mode != 'L':
secret = secret.convert('L')
# Cycle through pixels
for x in range(0, width):
for y in range(0, height):
shareA_colors = [0, 0, 0, 0]
shareB_colors = [0, 0, 0, 0]
for b in range(8):
pattern = random.choice(patterns)
if secret.getpixel((x, y)) >> b & 1:
for i in range(len(shareA_colors)):
shareA_colors[i] |= (pattern[i] << b)
shareB_colors[i] = shareA_colors[i]
else:
for i in range(len(shareA_colors)):
shareA_colors[i] |= (pattern[i] << b)
shareB_colors[i] |= ((1-pattern[i]) << b)
_draw_block(draw_A, (x, y), shareA_colors)
_draw_block(draw_B, (x, y), shareB_colors)La decifratura è pressoché simile allo schema di Naor-Shamir:
# Overlap shares to get the secret
secret = Image.new('L', share_A.size)
secret_draw = ImageDraw.Draw(secret)
for x in range(secret.size[0]):
for y in range(secret.size[1]):
p1 = share_A.getpixel((x, y))
p2 = share_B.getpixel((x, y))
secret_draw.point((x, y), p1 & p2)I risultati ottenuti con questo schema sono, per 7 bit in più di motivi, migliori del caso proposto precedentemente.
RGB VC

La crittografia visuale è applicabile anche ad immagini a colori, a patto di qualche precisazione. In questo caso, infatti, non parleremo di crittografia visuale nel senso "puro" del termine, ma abbiamo l'aggiunta di una tecnica che spesso viene confusa con la crittografia: la steganografia. Questa consiste nel nascondere - attenzione che nascondere non significa cifrare nel senso crittografico del termine! - le informazioni per una comunicazione fra interlocutori. Per le immagini a colori, nell'articolo Extended visual cryptography techniques for true color images, Dhiman e Kasana propongono due metodologie lossless (senza perdita di qualità) che mescolano steganografia a crittografia visuale. Si osservi che a tal proposito si parla di Tecniche di Crittografia Visuale Estesa (EVCT). Gli schemi proposti dagli autori sono classificabili come schemi a soglia, definiti come EVCT(N, N) e EVCT(K, N), con K<N. In particolare, si ha N=3 e K =2.
Ricordiamo che un'immagine a colori nello spazio RGB è costituita dai tre canali Red, Green e Blue. In EVCT(3, 3) il primo share contiene la componente R, il secondo share contiene la componente G e, infine, l'ultimo share contiene la componente B dell'immagine di partenza. Tutti e tre i crittogrammi - più in generale tutti gli N - sono necessari per poter ricostruire l'immagine nascosta. Nel caso di EVCT(2, 3) sono, invece, necessari solo due fra i tre share per poter effettuare la ricostruzione del segreto. Infatti, il primo share contiene le componenti RG, il secondo le componenti GB e il terzo le componenti RB dell'immagine di partenza. È facilmente intuibile dunque che in entrambi gli schemi gli share risultano significativi, in quanto contengono le immagini "cover" e le informazioni sull'immagine segreta. Il ruolo delle cover consiste nell'evitare eventuali sospetti che vi sia qualcosa nascosto all'interno. A tal proposito osserviamo che, nel caso della nostra implementazione, facciamo uso di LoremPicsum, un servizio gratuito dal quale scarichiamo delle cover random delle stesse dimensioni dell'immagine di input. Prima di procedere è bene precisare che gli schemi Dhiman-Kasana sono abbastanza onerosi in termini di prestazioni, poichè il size multiplier è di 5 (ogni pixel viene scomposto in un blocco 5x5). Le componenti vengono, in particolare, distribuite come mostrato in figura:
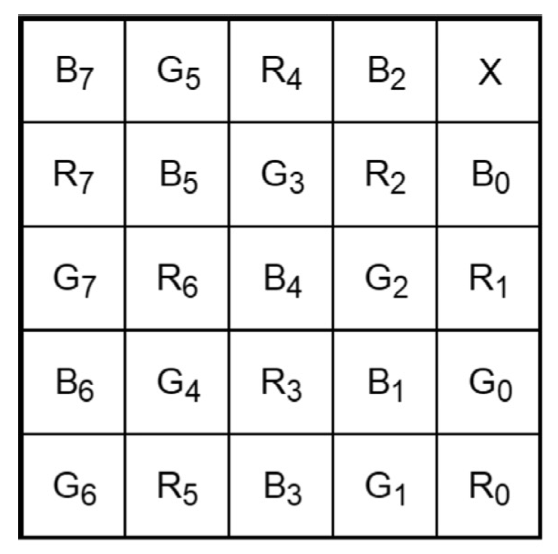
L'ultimo pixel in alto a destra viene lasciato invariato. Per semplicità illustreremo solamente gli algoritmi dello schema EVCT(N, N), in quanto nel caso dello schema (K,N) si tratta di seguire lo stesso ragionamento ma includendo le informazioni di due canali per volta (RG, GB, RB) in ogni share - ricordiamo comunque che il codice completo è visionabile sul repository del progetto VCrypture.
L'algoritmo di cifratura costruisce un blocco 5x5 in ognuno dei tre share per ogni pixel dell'immagine originale, seguendo il pattern appena descritto. Procede poi riempiendo gli 8 bit di ciascun canale seguendo la regola secondo cui se un bit è 1 si deve riempire di colore nero, altrimenti di colore grigio scuro:
components = {
'R': ((4, 4),(4, 2),(3, 1),(2, 3),(2, 0),(1, 4),(1, 2),(0, 1)),
'G': ((4, 3),(3, 4),(3, 2),(2, 1),(1, 3),(1, 0),(0, 4),(0, 2)),
'B': ((4, 1),(3, 3),(3, 0),(2, 4),(2, 2),(1, 1),(0, 3),(0, 0))
}
def _enc_bit(secret_bit: bool) -> Tuple[int, int, int]:
return (0, 0, 0) if secret_bit else (30, 30, 30)
x = 0
for i in range(width):
y = 0
for j in range(height):
secret_pixel = secret.getpixel((i, j))
for index, channel in enumerate(components.keys()):
cover_pixel = covers[index].getpixel((i, j))
with Image.new('RGB', (5, 5), cover_pixel) as block:
block_draw = ImageDraw.Draw(block)
for b, cell in enumerate(components[channel]):
block_draw.point(cell,
_enc_bit(secret_pixel[index] >> b & 1))
shares[index].paste(block, (x, y, x + 5, y + 5))
y += 5
x += 5L'algoritmo di decifratura utilizza l'operatore XOR per sovrapporre i tre share ed estrarre le informazioni dell'immagine segreta contenute nei blocchi 5x5 delle tre componenti RGB:
def _dec_bit(secret_pixel: Tuple[int, int, int]) -> bool:
return secret_pixel == (0, 0, 0)
for cover in covers:
ch = cover.info['CH']
ch_index = 0 if ch == 'R' else 1 if ch == 'G' else 2
x = 0
for i in range(0, width, 5):
y = 0
for j in range(0, height, 5):
sub = cover.crop((i, j, i + 5, j + 5))
color = 0
for b, cell in enumerate(components[ch]):
color |= _dec_bit(sub.getpixel(cell)) << b
s_color = list(secret.getpixel((x, y)))
s_color[ch_index] = color
secret_draw.point((x, y), tuple(s_color))
y += 1
x += 1Gli schemi proposti da Dhiman e Kasana risultano i migliori tra quelli illustrati in questo articolo, poichè presentano degli algoritmi lossless dai quali è possibile ricostruire l'immagine di partenza così com'era. Ciò ha però un prezzo in termini di prestazioni temporali e fa uso di steganografia, la quale influenza gli algoritmi nell'essere deterministici.
Conclusioni
La crittografia visuale rappresenta una tecnica interessante e molto potente. Grazie alla varietà di schemi è possibile sfruttarne le caratteristiche per più tipi di immagini, dalle immagini binarie per le quali abbiamo illustrato l'algoritmo Naor-Shamir, alle immagini a scala di grigi con l'algoritmo Taghaddos-Latif, per concludere con le immagini a colori con i due schemi di crittografia visuale estesa introdotti da Dhiman-Kasana. Le applicazioni della Visual Cryptography possono essere diverse. Fra queste possiamo menzionare: autenticazione cliente-banca, ricevute verificabili in e-voting, condivisione di immagini mediche. Nel primo caso la banca manda al cliente lo share chiave su vinile e pubblica in rete lo share crittogramma, così l'utente decodifica e legge la password. Nel caso dell'e-voting, chi ha votato riceve uno share della ricevuta. Per quanto riguarda le immagini mediche, l'utilizzo di schemi di crittografia visuale permette certamente di preservare la confidenzialità di informazioni sensibili. In ognuno di questi casi, il sistema visivo umano può risultare certamente più sicuro e affidabile di qualunque dispositivo digitale esistente.
References
- https://it.wikipedia.org/wiki/Crittografia_visuale
- Naor-Shamir: http://www.fe.infn.it/u/filimanto/scienza/webkrypto/visualdecryption.pdf
- Taghaddos-Latif: http://bit.kuas.edu.tw/~jihmsp/2014/vol5/JIH-MSP-2014-01-010.pdf
- Dhiman-Kasana: https://www.researchgate.net/publication/320228229_Extended_visual_cryptography_techniques_for_true_color_images
- VCrypture Repo: https://github.com/UniCT-WebDevelopment/VCrypture

